2.8 二叉平衡树
什么是平衡二叉树?
平衡二叉树(Balanced Binary Tree),由前苏联数学家G. M. Adelson-Velsky和Evgenii Landis在他们1962年的论文《An algorithm for the organization of information》中提出,因此也叫AVL树。
它是具有如下性质的树:
- 可以是一棵空树
- 可以是一颗左子树和右子树都是平衡二叉树且左右子树的深度之差的绝对值不超过1。
简单理解平衡二叉树
上文也出现了递归定义,可以不严谨的理解为:要么是一棵空树,要么是一棵平衡二叉树,在这棵树中,以任意节点为根作为一棵新树,那么这棵新树也得是二叉平衡树。
二叉平衡树是对二叉搜索树的改进,为什么要改进二叉搜索树?
假如有一棵二叉搜索树(BST),且为一棵空树。
当我们插入一组升序数据[1, 3, 5, 7, 9],BST1是这样的:

当我们插入一组降序数据[10, 8, 6, 4, 2],BST2是这样的:

那么请问这两棵树是二叉搜索树吗?的确是,完全符合二叉搜索树的性质。但毫无疑问,看上去更像是个链表。确实,当插入一组有序数据时,二叉搜索树退化成了链表,此时的查找效率退化为O(N)。
平衡因子
平衡因子(Balance Factor, BF)是某个节点左子树和右子树的高度之差(有的说法也叫深度之差,都是表达一个意思),一棵平衡二叉树的所有节点的平衡因子都只可能是0、-1、1。这一点也可以用来验证一棵二叉树是否为平衡二叉树。因为只要某二叉树的某个节点平衡因子大于1,那么该二叉树就一定不会是平衡二叉树。
如下由一棵平衡二叉树:

其中H表示高度(height),L表示左子树高度(Left height),R表示右子树高度(Right height), BF是平衡因子(Balance Factor, BF=L-R)。
如下有一棵非二叉平衡树:

其中根节点的平衡因子绝对值大于1,出现了“失衡”。
从非平衡二叉树到平衡二叉树
如何创建一棵平衡二叉树呢?由于平衡二叉树是对二叉搜索树的改进,所以在做插入操作的时候,我们仍然按照二叉搜索树的方式:找到要插入的位置并进行插入。然后如果该树中出现了平衡因子绝对值大于1的节点,就说明该调整了。我们把离插入节点最近且平衡因子绝对值大于1的祖先节点,以该节点为根的子树称为最小不平衡子树。首先要调整的就是这棵子树。
假如我们要插入一组数据[2, 1, 0]
相继插入,2和1后,树是这样的:

此时,并没有出现不平衡的情况,可以看作是一棵平衡二叉树。
但是插入0之后,就是图4那样了,根节点的平衡因子为2。我们以根节点2为根节点的树叫做最小不平衡子树,情况特殊,因为此时根节点出现了失衡,所以最小不平衡子树是它本身。
如下图的一棵非二叉平衡树,

可以看到,在插入节点53之后,节点24和节点37的BF绝对值都大于1,但我们把以节点37为根的树叫做最小不平衡子树,因为它离刚插入的节点53最近。
平衡二叉树与其节点的表示
/* 平衡二叉树的节点 */
typedef struct avl_node {
/* 关键字 */
int key;
/* 左右节点指针 */
struct avl_node *left;
struct avl_node *right;
/* 节点的高度 */
int height;
}avl_node;
/* 平衡树二叉树本身 */
typedef struct avl {
/* 指向二叉树根节点 */
struct avl_node *root;
/* 树的节点数 */
int size;
}avl;
平衡二叉树及其节点的创建
/* 创建一个节点 */
avl_node *avl_create_node(int key)
{
avl_node *node = (struct avl_node*)malloc(sizeof(struct avl_node));
if(node==NULL) return NULL;
node->height = 1;
node->key = key;
node->left = NULL;
node->right = NULL;
return node;
}
/* 创建一棵平衡二叉树 */
avl *avl_create(void)
{
avl *avl = (struct avl*)malloc(sizeof(struct avl));
if(avl==NULL) return NULL;
avl->root = NULL;
avl->size = 0;
return avl;
}
节点的高度相关函数
/* 返回一个节点的高度 */
int avl_height(avl_node *node)
{
if(node==NULL) return 0;
return node->height;
}
/* 比较一个key和一个节点的key的大小
* 如果key比较大,返回真,否则返回假。
*/
int avl_compare_key(int key, avl_node *node)
{
if(node==NULL) return 0;
if(key > node->key) return 1;
return 0;
}
/* 返回两个节点中的高度较大值 */
int max(avl_node *x, avl_node *y)
{
int m = avl_height(x);
int n = avl_height(y);
return m>=n?m:n;
}
四种不平衡情况
一棵平衡二叉树在插入某个节点后失衡,只会出现四种不平衡类型。在每种不平衡类型中在处理不平衡的操作中,顺时针旋转,叫做右旋;逆时针旋转叫做左旋。
LL型
LL型可以看作是重心在Left,需要进行一次右旋操作。
/* LL型,需要向右旋 */
avl_node *avl_rotate_ll(avl_node *node)
{
/* 新的“根” */
avl_node *top = node->left;
node->left = top->right;
top->right = node;
/* 重新计算高度, 注意:node与top的高度计算次序千万不能颠倒 */
node->height = max(node->left, node->right) + 1;
top->height = max(top->left, top->right) + 1;
return top;
}
下图演示了最小不平衡子树是它本身(简称情况1):
找到最小不平衡子树(根节点31)后右旋。我们把最小不平衡子树的左子树作为新的top节点。

下图演示了最小不平衡子树的根不是二叉树的根,也即最小不平衡子树是二叉树的“真子树”(情况2)。类似于集合中的真子集。

RR型
/* RR型,需要向左旋 */
avl_node *avl_rotate_rr(avl_node *node)
{
avl_node *top = node->right;
node->right = top->left;
top->left = node;
/* 重新计算高度 */
node->height = max(node->left, node->right) + 1;
top->height = max(top->left, top->right) + 1;
return top;
}
情况1:

情况2:

LR型
假如对空树AVL插入一组数据[31, 25, 28]
相继插入31,25后没问题,接着插入28:

此时出现了以节点31为根节点的不平衡子树,既不是LL型,也不是RR型,而是LR型。需要进行两次操作,第一次对根节点的左子树左旋:

左旋后,可以发现,该子树变成了LL型,所以再对该子树进行右旋:

代码很简单(适用所有LR情况):
/* LR型,先左旋再右旋 */
avl_node *avl_balance_lr(avl_node *node)
{
node->left = avl_rotate_rr(node->left);
return avl_rotate_ll(node);
}
上面的图片和数据演示了LR(0)
下面演示LR(L)型:
插入前:

插入时:

如果插入的数据不是26,而是比28要大的数,那么此时应该插入在28的右子树,则为LR(R)型,不再演示。
插入后:

动图演示:

RL型
于LR型相反,先对最小不平衡子树的右子树右旋,在对最小不平衡子树左旋即可。
/* RL型,先右旋再左旋 */
avl_node *avl_balance_rl(avl_node *node)
{
node->right = avl_rotate_ll(node->right);
return avl_rotate_rr(node);
}
对于RL(L)型,插入前:

插入时:
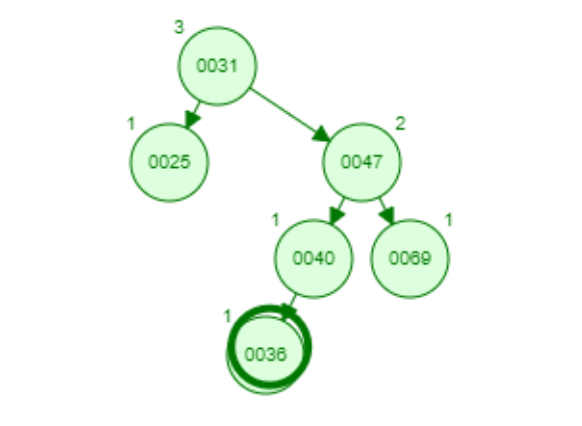
如果插入的不是36,而是比40大的,比如43。那么应该插入在40的右子树,此时就是RL(R)型,不再演示。
插入后:

动图演示:

不平衡的调整方法
在很多资料中,调整的方法都是递归的,但是我不喜欢递归,所以就介绍更加符合线性思维的非递归插入方法(其实本质上还是递归,只是用栈模拟了)。
说说我的调整思路:
- 插入某个节点时,插入方法同二叉搜索树,并且将该节点高度为1。
- 记录插入某个节点时,要经过的节点。比如在图6中,要插入节点53,要经过的节点就是 24 - 37 - 90。
- 把它们依次放到栈中,根据栈先进后出的特点,出栈顺序应该是90 -> 37 -> 24。
- 出栈一个节点,首先调整该节点高度。调整方法为:取该节点的左子树与右子树高度的较大值然后加1。
- 如果该节点有父节点,按照同样的方法调整父节点高度。
- 最后计算一下该节点的平衡因子BF。
- 若该节点BF绝对值大于1,则判断对应的不平衡情况并调整。
- 出栈下一个节点,并回到步骤4,直到栈空。
/* 平衡树二叉树,插入一个节点 */
avl *avl_insert_node(avl *avl, int key)
{
stack *stack = stack_create();
avl_node *current, *parent;
current = avl->root;
/* 如果是空树则直接插入 */
if(current==NULL) {
avl->root = avl_create_node(key);
avl->size++;
stack_release(stack);
return avl;
}
/* 找到待插入节点的位置,同时将路过的节点放入栈中 */
while (current != NULL)
{
stack_push(stack, current);
if(key < current->key) {
parent = current;
current = current->left;
} else if(key == current->key) {
break;
} else{
parent = current;
current = current->right;
}
}
/* 插入节点 */
if(key < parent->key) {
parent->left = avl_create_node(key);
} else if(key == parent->key) {
stack_release(stack);
return NULL;
} else {
parent->right = avl_create_node(key);
}
/* 回溯经过的节点,判断是否需要调整 */
while (stack->length)
{
current = stack_pop(stack);
/* 注意:这里只是取栈顶元素,并没有出栈 */
parent = stack->top == NULL ? NULL : stack->top->data;
/* 调整高度 */
current->height = max(current->left, current->right) + 1;
/* 计算平衡因子 (balance factor) */
int bf = avl_height(current->left) - avl_height(current->right);
printf("回退:%d, left: %d , right: %d , bf: %d\n", current->key, avl_height(current->left), avl_height(current->right), bf);
/* 可能是RR或者RL型 */
if(bf == -2) {
/* 如果插入key比当前最小不平衡子树的右子树key大,则是RR型 */
if(avl_compare_key(key, current->right)) {
/* 最小不平衡子树,是否有父节点 */
if(parent == NULL){
avl->root = avl_rotate_rr(current);
} else {
/* 如果有父节点,则需要判断,该最小不平衡子树属于父节点的左子树还是右子树 */
if(current->key > parent->key) {
parent->right = avl_rotate_rr(current);
} else {
parent->left = avl_rotate_rr(current);
}
}
}
/* 否则就是RL型 */
else {
if(parent==NULL) {
avl->root = avl_balance_rl(current);
} else {
if(current->key > parent->key) {
parent->right = avl_balance_rl(current);
} else {
parent->left = avl_balance_rl(current);
}
}
}
}
else if(bf==2) {
/* LR型 */
if(avl_compare_key(key, current->left)) {
if(parent==NULL) {
avl->root = avl_balance_lr(current);
} else {
if(current->key > parent->key) {
parent->right = avl_balance_lr(current);
} else {
parent->left = avl_balance_lr(current);
}
}
}
/* LL型 */
else {
if(parent==NULL) {
avl->root = avl_rotate_ll(current);
} else {
if(current->key > parent->key) {
parent->right = avl_rotate_ll(current);
} else {
parent->left = avl_rotate_ll(current);
}
}
}
}
if(parent != NULL) {
parent->height = max(parent->left, parent->right) + 1;
}
}
avl->size++;
stack_release(stack);
return avl;
}
在main函数中测试
int main()
{
avl *avl = avl_create();
int arr[] = {21, 3, 5, 26, 29, 50, 18, 53, 8, 67, 1, 78, 6};
//int arr[] = { 21, 3, 5, 26, 29, 50};
int length = sizeof(arr) / sizeof(int);
int i;
for(i=0;i<length;i++) {
printf("--------\n");
printf("插入:%d\n", arr[i]);
avl_insert_node(avl, arr[i]);
printf("中序: ");
avl_inorder_traversal(avl->root);
printf("\n");
}
return 0;
}
编译运行
#gcc *.c && ./a.out
--------
插入:21
中序: 21
--------
插入:3
回退:21, left: 1 , right: 0 , bf: 1
中序: 3 21
--------
插入:5
回退:3, left: 0 , right: 1 , bf: -1
回退:21, left: 2 , right: 0 , bf: 2
中序: 3 5 21
--------
插入:26
回退:21, left: 0 , right: 1 , bf: -1
回退:5, left: 1 , right: 2 , bf: -1
中序: 3 5 21 26
--------
插入:29
回退:26, left: 0 , right: 1 , bf: -1
回退:21, left: 0 , right: 2 , bf: -2
回退:5, left: 1 , right: 2 , bf: -1
中序: 3 5 21 26 29
--------
插入:50
回退:29, left: 0 , right: 1 , bf: -1
回退:26, left: 1 , right: 2 , bf: -1
回退:5, left: 1 , right: 3 , bf: -2
中序: 3 5 21 26 29 50
--------
插入:18
回退:21, left: 1 , right: 0 , bf: 1
回退:5, left: 1 , right: 2 , bf: -1
回退:26, left: 3 , right: 2 , bf: 1
中序: 3 5 18 21 26 29 50
--------
插入:53
回退:50, left: 0 , right: 1 , bf: -1
回退:29, left: 0 , right: 2 , bf: -2
回退:26, left: 3 , right: 2 , bf: 1
中序: 3 5 18 21 26 29 5053
--------
插入:8
回退:18, left: 1 , right: 0 , bf: 1
回退:21, left: 2 , right: 0 , bf: 2
回退:5, left: 1 , right: 2 , bf: -1
回退:26, left: 3 , right: 2 , bf: 1
中序: 3 5 8 18 21 26 2950 53
--------
插入:67
回退:53, left: 0 , right: 1 , bf: -1
回退:50, left: 1 , right: 2 , bf: -1
回退:26, left: 3 , right: 3 , bf: 0
中序: 3 5 8 18 21 26 2950 53 67
--------
插入:1
回退:3, left: 1 , right: 0 , bf: 1
回退:5, left: 2 , right: 2 , bf: 0
回退:26, left: 3 , right: 3 , bf: 0
中序: 1 3 5 8 18 21 2629 50 53 67
--------
插入:78
回退:67, left: 0 , right: 1 , bf: -1
回退:53, left: 0 , right: 2 , bf: -2
回退:50, left: 1 , right: 2 , bf: -1
回退:26, left: 3 , right: 3 , bf: 0
中序: 1 3 5 8 18 21 2629 50 53 67 78
--------
插入:6
回退:8, left: 1 , right: 0 , bf: 1
回退:18, left: 2 , right: 1 , bf: 1
回退:5, left: 2 , right: 3 , bf: -1
回退:26, left: 4 , right: 3 , bf: 1
中序: 1 3 5 6 8 18 2126 29 50 53 67 78
完整代码,请详见代码清单。